Razonamiento lógico y conjuntos

Razonamiento matemáticos

Propósito: Ejercitar al estudiante para adquirir la competencia en el razonamiento matemático.

¿En que consiste la competencia en el razonamiento matemático?

Esta habilidad consiste en utilizar y relacionar los números, las operaciones básica y la resolución de problemas con la vida cotidiana para analizar e interpretar distintos tipos de información que "ayudan a comprender que las matemáticas no son simplemente una memorización de reglas y algoritmos, sino que tienen sentido, son lógicas, potencian la capacidad de pensar y son divertidas" (Estándares básicos de competencias matemáticas)

Anécdota

El príncipe de las matemáticas: Gauss

Johann Carl Friedrich Gauss niño genio

Haz click y aprende algo más sobre Gauss

https://www.um.es/docencia/pherrero/mathis/gauss/gau.htm

Actividad: Piensa y plantea una estrategia rápida para calcular:
1. La suma de los diez primeros números naturales
2. La suma de los 50 primeros números naturales?

Diviértete y aprovecha el tiempo libre

Asume el reto interactivo y juega

Haz click en el siguiente enlace y allí encontraras la siguiente imagen http://www.actiludis.com/wp-content/uploads/2009/11/triangulo.swf

Asume el reto y envía la solución al correo electrónico y gana un salvavidas.

1. Con los números del 1 al 6 llena los círculos de la siguiente figura de manera que la suma de cada lado sea 9 y cada dígito se utilice sólo una vez.

Actividad tomado de: http://matematicassextouno.blogspot.com.co/2014/02/guia-2-razonamiento-numérico-sucesiones.html

Ejercicios de razonamiento lógico y polinomios aritméticos

Plantea  las operaciones y luego calcula el valor indicado.

Ejercicio tomado del siguiente enlace 

https://www.smartick.es/blog/matematicas/logica/ejercicios-logica-smartick-2/

Averigua el valor de cada fruta y plantea la operación

Averigua el valor de cada pizza y cada porción 

Juegos interactivos

Plante las operaciones o polinomios aritméticos y resuelve. Luego verifica la respuesta

Haz click http://www.elclubdelingenio.com.ar/un-juego-de-logica-razonamiento-y-calculo/

Propósito: Afianzar las operaciones básicas en el conjunto de los números naturales.

Acertijos matemáticos

Acertijo para resolver en familia

El pez con palillos

Cuadrado mágico

Propósito: Afianzar la adición y su operación inversa a través del juego

Busca la solución y haz click en cada uno para encontrar la respuesta y diviértete. 

http://www.ceibal.edu.uy/UserFiles/P0001/ODEA/ORIGINAL/110523_cuadrados_magicos.elp/qu_es_un_cuadrado_mgico.html

a.¿Qué es un cuadrado mágico?
b. Cuenta un poco sobre la historia....
c. Haz click en cada uno: Tipos de cuadrados mágicos, completa, casilla central y líneas.

d. Envía el pantallazo del reto resuelto y gana puntos en participación

El reto es disfrutar el juego interactivo del cuadrado mágico. Haz click 

      http://www.disfrutalasmatematicas.com/juegos/juego-del-cuadrado-magico.html

¿Quien me puede ayudar a resolver un cuadrado mágico?. 

Aquí encontraras la explicación

Aprende jugando con las balanzas

Haz click en el siguiente enlace selecciona el juego con balanzas y plantea la estrategia para solucionar el ejercicio de razonamiento lógico.

http://ntic.educacion.es/w3/eos/MaterialesEducativos/mem2011/razonamiento_logico/actividades/rl.html

También puedes encontrar otros juego. Espero que te diviertas mucho y pases los diferentes niveles.

Lógica

Tema: Proposiciones lógicas

El delfín rosado del amazonas

Observa el vídeo, realiza un comentario sobre este y escribe tres oraciones 

El ornitorrinco de Australia

Observa el vídeo y escribe las características que tiene este animal.

 2. ¿Por qué  se considera una criatura asombrosa y para otros extraña?

 3. Escribe 2 oraciones con la información anterior. 

 4. Observa el vídeo y descubre si el equidna tiene características similares al ornitorrinco

¿Cómo identificar una proposición simple?

Después de complementar la explicación a través del vídeo realiza la actividad planteada.

¿Cuál es la diferencia entre una proposición simple y una proposición compuesta?

Recuerda contestar la pregunta en los comentarios para que todos podamos aprender de manera colaborativa. Todos los aportes son interesantes e importantes.

Negación de una proposición simple

Conectores lógicos 

Mediante el uso de partículas de enlace se puede, a partir de proposiciones simples, formar proposiciones compuestas.

Observa la tabla con el nombre del conectivo y su respectivo símbolo
Tomado de:http://matematicaslito.blogspot.com/p/logica-y-conjuntos.html

                                            

Ejemplo:

Proposiciones simples

p: 5 es un número primo 

q: 8 es múltiplo de 2 

Proposición compuesta

5 es un número primo y 8 es múltiplo de 2

5 es un número primo o 8 es múltiplo de 2.

Conectivos lógicos y tablas de verdad

Complementa la explicación de la clase y aplica los conceptos

Taller de profundización

Lógica y conjuntos

 Te invito a profundizar el tema y ampliar tus conocimientos en el 2017

Conjuntos

Observa las siguientes imágenes y piensa que es lo que tienen en común

                         

Tomado de gif animados

En este caso tenemos un conjunto de personas que practican un deporte.

¿Qué es un conjunto? Es la reunión o colección de personas, animales, objetos entre otros, llamados elementos, con alguna característica especifica en común. Los conjuntos, normalmente, se representan con letras mayúsculas.

Ejemplos:

El equipo de baloncesto

El conjunto de los números naturales

El conjunto de las vocales

Observa un  conjuntos de mariposas

Tomado de: http://www.freepik.es/index.phpgoto=41&idd=676850&url=aHR0cDovL3d3dy53ZWJkZXNpZ25ob3QuY29tL2ZyZWUtdm

Los conjuntos en la  música y en el  reciclaje 

Observa el vídeo y escribe cuales crees que son  las característica comunes de este conjuntos.

Clases de conjuntos

Propósito: Clasificar los conjuntos según el número de elementos y caracteristicas.

Analicemos cada uno de los siguientes conjuntos

Conjunto universal o Referencial: Es cuando contiene a todos los conjuntos dados en una situación determinada.

Ejemplo:

El conjunto delos animales mamíferos es el conjunto Universal o referencial.

Se pueden formar varios subconjuntos como:

• Animales mamíferos y ovíparos
• Animales mamíferos y acuáticos
• Te invito a encontrar otros subconjuntos

Conjunto finito: Es aquel en el que podemos enumerar todos sus elementos.

Ejemplo: 

Conjunto infinito: Es aquel en el que no se pueden determinar la cantidad de elementos que conforman el conjunto.

Ejemplo:

El conjunto de los números naturales

B= { 1,2,3,4,5,6,7,8,9,10,11,12,13,14,...}

B= {x/x es un número natural}

Otro ejemplo serían las estrellas del universo

Imagen tomada de https://sincu.wordpress.com/tag/clases-de-conjuntos/

Conjunto unitario: Es el conjunto que sólo tiene un elemento.

Ejemplo: 

Consulta y responde la siguiente pregunta:

a.¿Existe en el mundo otro animal con pico de pato, patas de nutria y cola de castor?

b.¿Por que crees que es conjunto unitario?

Conjunto Vacío: Es el conjunto que no tiene elementos y se representa con el símbolo Ø    También se puede representar así: O = {  }

Ejemplo

A = { estudiante de 6° de la Institución Educativa la Paz con 18 años}

Participa: En los comentarios escriba ejemplos de un conjunto vacío.

Propósito: Determinar los conjuntos por extensión y por comprensión 

  Actividad

Observa las imágenes y determina el conjunto por extensión y por comprensión. Puedes enviar la respuesta al correo o la escribe en los comentarios con el nombre y grupo.

Imagen tomado de: https://imaso55.wordpress.com/2013/03/ 

b. Expresa por extensión: El conjunto de los números primos menores o igual a 100.

 B= {

Pista para identificar los números primos con la criba de Eratóstenes 

Ejemplo 

U={ x/x es un número natural menor que 11}

U={ 1,2, 3, 4, 5, 6, 7, 8, 9, 10}

A es un subconjunto del conjunto Universal o Referencial 

Ejemplo:

Actividad

Observa y responde

a. Determina el conjunto universal por extensión

b. El subconjunto T es el tiburón toro.

C. Realiza la lectura sobre el tiburón toro y luego escribe 2 proposiciones simples y finalmente escribe una proposición compuesta con su respectiva  notación y  valor de verdad con relación a su habitad .( Participa y escribe la respuesta en los comentarios )

Haz clic 
http://www.opepa.org/index.php?option=com_content&task=view&id=522&Itemid=29 

U={

A={

B={

b.Identifica cual es el conjunto universal o referencial y los subconjuntos, luego clasifica cada conjunto según su número de elementos y finalmente los determina por comprensión.
( Escribe la respuesta en los comentarios o lo envía al correo)

¿Cómo se representan los conjuntos en un diagrama de Venn

Taller de aprendizaje

Propósito: Aplicar los conceptos de conjuntos en la resolución de problemas.
Observa el vídeo y amplia la explicación de la clase

Relación entre conjuntos

Entre los conjuntos se establece la relación de pertenencia y de inclusión así:

Relación de pertenencia

Haz clic: Encontraras la explicación: http://es.slideshare.net/greenangelvv/relacin-de-pertenencia-e-inclusin.

El ejercicio es  tomado del  enlace anterior y puedes enviar la respuesta al correo y ganas puntos por participación.

Relación de igualdad
Tomado de: https://www.slideshare.net/greenangelvv/relacin-de-pertenencia-e-inclusin

Recordemos:

• La relación de pertenencia se realiza entre: Un elemento a un conjunto.

• La relación de inclusión se realiza entre:  Un conjunto a conjunto.

Operaciones entre conjuntos

Sean, U el conjunto universal o referencia y A, B dos conjuntos, se puede definir entre ellos las siguientes operaciones: Unión, intersección, complemento, diferencia y diferencia simétrica. 

Unión entre conjuntos
La unión de dos conjuntos A y B, es el conjunto formado por los elementos que pertenecen tanto al conjunto A como a B. La unión de dos conjuntos A y B se denota A U B.

Se lee: A o B

Formalmente se define como:

A U B = { x / x pertenece a A o x pertenece a B}   también se puede expresar así:

Ejemplo 1: Representa en el diagrama de Venn

• Puedes participar escribiendo la respuesta en los comentarios o la puedes enviar al correo.
• Realiza la actividad interactiva para afianzar lo aprendido en clase. 

Haz click: http://www.thatquiz.org/es-p/?-j4110-l1-p0  
             

Intersección entre conjuntos

La intersección de los conjuntos A y B, es el conjunto formado por todos los elementos comunes entre los conjuntos A y B. La intersección de dos conjuntos A y B se nota A 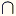 B.

Se lee: A y B

Formalmente se define como:
A 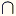 B ={x/x pertenece a A y x pertenece a B}

Se representa gráficamente en el diagrama de Venn así: 

Tomado de:http://matematica1.com/teoria-y-operaciones-con-conjuntos-ejercicios-de-sexto-grado-de-primaria-pdf/

Representa en el digrama de Venn

Actividad

Ingresa al siguiente enlace http://animalesoviparos.com/animales-mamiferos-oviparos/ y responde la pregunta que ellos plantean: ¿Cómo es eso de que existen animales mamíferos que a la vez son ovíparos?, luego determina los  conjuntos por extensión y escribe cuatro animales que cumplan la característica de cada conjunto. Finalmente representa la información en el diagrama de Venn y halla la intersección de los conjuntos.

P= {x/x es un animal ovíparo}

P= {

Q={ x/x es un animal mamífero}

Q= {

P y Q   indica que:  x es un animal mamífero y ovíparo.

Complemento de un conjunto.

El complemento de un conjunto A contenido en un conjunto Universal o referencial U, es el conjunto formado por todos los elementos que pertenecen al conjunto Universal y no pertenece al conjunto A. El complemento de nota 

Formalmente se define como: 

Representación en el diagrama de Venn 

                                                                     

Ejemplo:

Diferencia entre conjuntos

La diferencia de los conjuntos A y B, es el conjunto formado por todos los elementos que pertenecen al conjunto A pero no pertenecen al conjunto B. La diferencia entre los conjuntos A y B. Se nota

 Formalmente se define como:

Representa en el diagrama de Venn 

Representa en el diagrama de Venn   B - A

Diferencia simétrica

La diferencia simétrica de los conjuntos A y B, es el conjunto formado por todos los elementos que pertenecen a la unión de A y B y no pertenecen a la intersección entre A y B.La diferencia simétrica se nota  

Formalmente se defines como:

Representa en el diagrama de Venn la diferencia simétrica

Bibliografía: Nuevas matemáticas 6° (Aritmética, geometría y estadística) de Santillana.
Supermat 6°, Alfa 6° y 7°, contextos de santillana, libros del Ministerio de Educación Nacional.